نظم المعادلات الخطية والغير الخطية

المعادلات الخطية: هي المعادلات التي تحتوي على أكثر من متغير من الدرجة الأولى، ولا تحتوي تلك المعادلات على متغيرات بدرجة أعلى، جذور، دوال مثلثية، أو ضرب متغيرات مع بعضها البعض، أو دوال أسية، إذاً يمكن عدّها أبسط تركيب المعادلات، ويتم خلها بطرق تعد بسيطة نسبياً، كتبادل معادلتين لبعضهما، أو ضرب معادلة بثابت غير صفري، أو جمع مضاعف إحدى المعادلات الى أخرى.

أما المعادلات الغير خطية: فهي تحتوي على متغيرات من درجات أعلى من الواحد، وبإمكانها الاحتواء على جذور ودوال مثلثية ودوال أسية والخ.... ( Bradford، 2018)

ماهي نظم المعادلات الخطية والغير خطية التي تستطيع أن تتخيلهم؟

المعادلات الخطية:

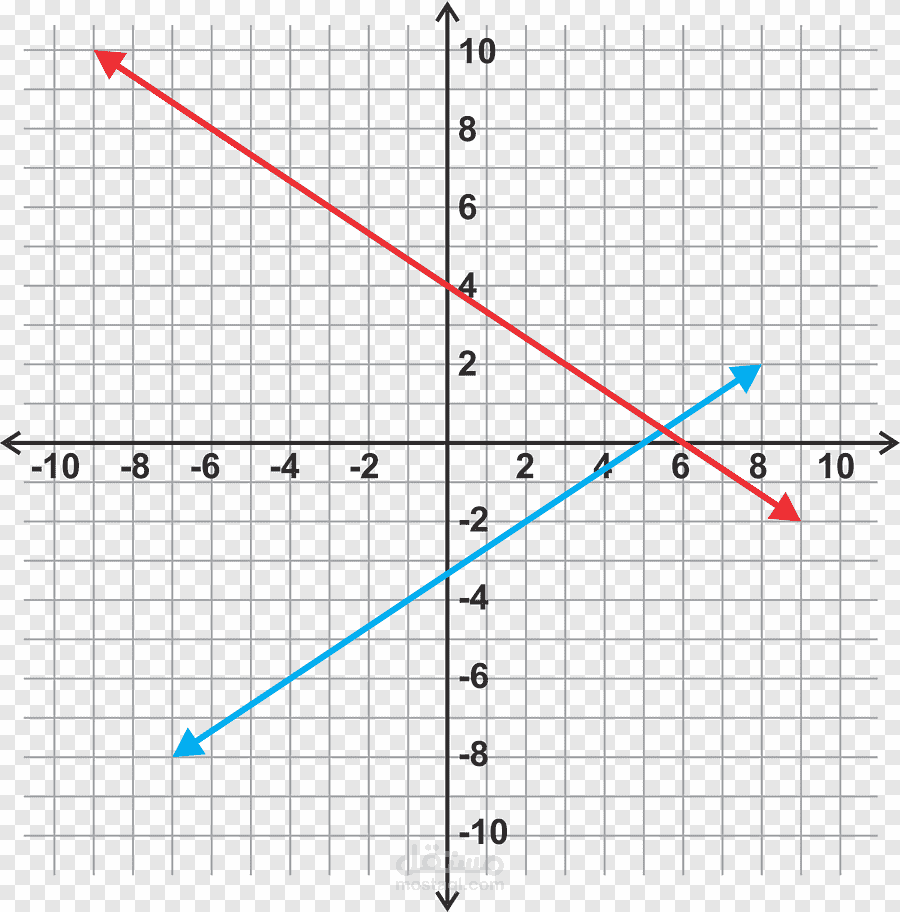
فيمكن أن نتخيل معادلتين بمجهولين بالشكل التالي:

x+y=-1

2x-y=4

وعند حل المعادلتين بتعويض قيمة أحد المتغيرين، بالآخر نحصل على القيم التالية:

y=-2

x=1

المعادلات غير الخطية:

يمكن أن نتخيل جملة المعادلتين التاليتين:

x^2-y=1

y+cosx=0

ولا يمكن حلها بالطريقة السابقة التي تم حل المعادلات الخطية من خلالها.

وبالتأكيد يوجد حقائق عديدة يمكن من خلالها تفسير نظم المعادلات الخطية والغير خطية نذكر منها:

فالمعادلات الخطية: يمكن استخدامها في مجالات عديدة كالهندسة والعلوم، وتطبيقات مختلفة كتحديد تكلفة المنتج بناءً على عدد الوحدات المنتجة، والتنبؤ بالمبيعات المستقبلية بناءً على البيانات السابقة، ونمذجة مسار المقذوف. (faster capital،2024)

وفي مثال على معادلة خطية تستخدم في معادلات النواسات لحساب نبض الحركة بدلالة التواتر، فنكتب المعادلة بالشكل التالي:

ω=2π f

حيث أن:

ω تمثل نبض الزاوية

2πتمثل مقدار ثابت يعطى بالقيمة 3.14

fتمثل تواتر الحركة

اما المعادلات غير الخطية:

فمجالاتها عديدة في الهندسة والعلوم والاقتصاد والعديد من المجالات الأخرى، وفي ذكر مثال على إحدى المعادلات غير الخطية في مجال الفيزياء، يمكن استعراض علاقة الدور T_0 في النواس الثقلي:

T_0=2π√(I_∆/mgd)

حيث ان:

I_∆هي عزم عطالة الجسم (الجملة المدروسة)

mكتلة الجسم

gالجاذبية الأرضية

d البعد بين محور الدوران ومركز ثقل جملة النواس الثقلي.

2πتمثل مقدار ثابت يعطى بالقيمة 3.14